N皇后问题（递归解法）

描述

​ 在N*N的棋盘上摆N个皇后，要求任何两个皇后不同行、不同列、不同斜线，问有多少种摆法。

​ 如，N=1时，只能摆一个，一种摆法。

​ N=2和3时，没法摆，0种摆法。

​ N=8时，92种摆法。

常规方法

基本思路

1. 一行一行摆，从第一行开始，找满足条件的位置（保证与已记录的坐标不同列、不同斜线），摆好后记录坐标；
2. 如果来到了最后一行，根据前面摆好的位置，计算最后一行的摆法并返回，然后上一层继续对满足条件的位置循环，循环完，返回累加的结果。

实现思路

1. 准备一个 record 一维数组，record[i]表示第 i 行的皇后在第几列
2. 设计递归方法process()，参数为目前来到的行号i、之前行的皇后的位置record[]、总共的行数n，返回值为多少种摆法，递归终止条件为当前行i == n（最后一行找到了位置调用了递归，递归下一行），返回1
3. 每行找到一个位置后，记录坐标，看下一行，往下递归，递归完了继续循环找位置。

实现代码

//n表示n行n列，n个皇后
public static void nQueens(int n){
    if(n < 1){
        return 0;
    }
    //放n个皇后的坐标
    int[] record = new int[n];
    //返回递归的结果
    return process(0,record,n);
}
//i：当前来到的行；record：之前行的皇后的坐标；n：皇后的总数
private static int process(int i, int[] record, int n){
    //递归出口
    if(i == n){
        return 1;
    }
    //记录摆法种数
    int res = 0;
    //找当前行符合条件的位置
    for(int j = 0; j < n; j++){
        //当前i行的皇后，放在j列，是否符合条件
        if(isValid(record,i,j)){
            //符合则记录下这个位置
            record[i] = j;
            //继续看下一行的位置
            res += process(i+1,record,n);
        }
    }
    //返回所有的摆法
    return res;
}
//判断在i行j列位置放皇后，是否满足条件
private static boolean isValid(int[] record,int i,int j){
    //与i行之前所有行的皇后进行对比
    for(int k = 0; k < i; k++){
        //是否在同一列或同一斜线（列减列 等于 行减行）
        if(j == record[k] || Math.abs(record[k] - j) == Math.abs(i -k)){
            return false;
        }
    }
    return true;
}

优化方法

基本思路

——只针对1~32皇后问题

​ 利用位运算。和常规方法类似，深度优先，确定了一个位置就往下，但是判断是否能放皇后不用去遍历上面所有皇后，而是用位运算，一行中每个位置都看做一个二进制位，为1表示放了皇后，0表示没放。

​ 如第一行为00010000，然后下一行受影响不能放皇后的位置有三个：当前位（00010000）、向左一位（00100000）、向右一位（00001000），三个位置与一下得到 00111000，再取反得到 11000111，1表示能放皇后的位置，0表示受影响不能放的位置，然后从右往左放皇后，放好后，进入下一行，并带上下一行受影响的位置：当前位与上当前行受影响的当前位即 00010001、当前位 与上 当前行受影响的向左位 再整体向左一位 即 01000010、当前位 与上 当前行受影响的向右位 再整体向右一位 即 00000100 。这样就可以把每行的皇后影响的位置层层保留传递下去。

​ 文字比较难懂，看图：

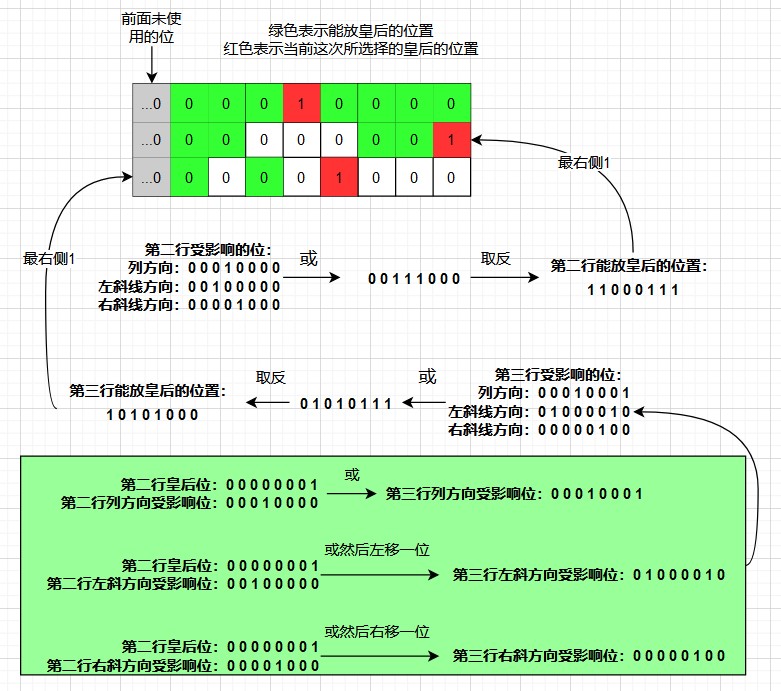
实现代码

//优化后的N皇后问题算法（通过位运算将受影响的位置层层累积传递下去）
public static void nQueensByBit(int n){
    //对于1~32皇后以外的问题不处理
    if(n < 1 || n > 32){
        return 0;
    }
    //几皇后问题设置几个1（总皇后数）
    int limit = n == 32 ? -1 : (1 << n) -1;
    return processByBit(limit,0,0,0);
}
//colLim：当前行受之前皇后同列方向影响的位
//leftDiaLim：当前行受之前皇后同左斜线方向影响的位
//rightDiaLim：当前行受之前皇后同右斜线方向影响的位
private static int processByBit(int limit, int colLim, int leftDiaLim, int rightDiaLim){
    //如果受列方向影响的位全为1，说明每行都放好了皇后，满足条件
    if(colLim == limit){
        return 1;
    }
    //根据影响计算能放皇后的位置（这里与上limit是为了把那些没用到的位经取反操作变为1了，再给它变回0）
    int pos = limit & (~(colLim | leftDiaLim | rightDiaLim));
    //记录从右往左找到的能放皇后的位置
    int mostRightOne = 0;
    //记录结果
    int res = 0;
    //遍历每个能放皇后的位置，处理完一个就去掉这位
    while(pos != 0){
        //找到最右侧能放皇后的位置（最右侧为1的位）
        mostRightOne = pos & (~pos + 1);
        //找到了就去掉这个位置（能放的位置 减去 这个位置）
        pos = pos - mostRightOne;
        //记录往下递归得到的结果，往下递归时带上这行受影响的位置
        res += processByBit(limit,
                            colLim | mostRightOne,
                            (leftDiaLim | mostRightOne) << 1,
                            (rightDiaLim | mostRightOne) >> 1);
    }
    return res;
}