二叉树的前序、中序、后序遍历

一、递归打印

几个顺序

例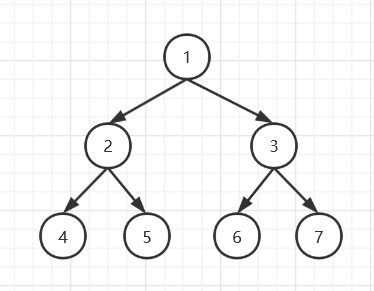： 对每个节点的左右节点进行递归，如下

public static void recursion(Node head){
    if(head == null){
        return;
    }
    //第1次打印
    recursion(head.left);
    //第2次打印
    recursion(head.right);
    //第3次打印
}

在递归左节点之前，可以第1次打印当前节点的值；当左节点递归结束后，代码继续往下执行，可以第2次打印当前节点；当右节点递归结束，代码继续往下执行，可以第3次打印当前节点，于是可以得到一个递归序，如下：

• **递归序：**1 2 4 4 4 2 5 5 5 2 1 3 6 6 6 3 7 7 7 3 1
• 先序遍历：1 2 4 5 3 6 7（递归序第一次出现的节点）
• 中序遍历：4 2 5 1 6 3 7（递归序第二次出现的节点）
• 后序遍历：4 5 2 6 7 3 1（递归序第三次出现的节点）

实现代码

/**
* 递归打印
* @param head 树的根节点
* @param printType 打印类型
*/
public static void recursion(Node head,String printType){
    if(head == null) return;
    //先序遍历打印处
    if("first".equals(printType)){
        System.out.print(head.value+" ");
    }
    recursion(head.left,printType);
    //中序遍历打印处
    if("mid".equals(printType)){
        System.out.print(head.value+" ");
    }
    recursion(head.right,printType);
    //后序遍历打印处
    if("last".equals(printType)){
        System.out.print(head.value+" ");
    }
}

二、非递归打印

利用栈

先序遍历：

1. 先将根节点压栈
2. 每次从栈中弹出一个节点cur
3. 打印（处理）cur节点
4. 先将cur的右节点压栈，后将cur左节点压栈（如果有左右节点）
5. 重复2~4过程直至栈为空

实现代码

public static void stackFirstPrint(Node cur){
    Stack<Node> stack = new Stack<Node>();
    stack.push(cur);//头结点先入栈
    while(!stack.isEmpty()){
        //弹出节点并打印
        cur = stack.pop();
        System.out.print(cur.value+" ");
        //先将右节点压栈
        if(cur.right!=null){
            stack.push(cur.right);
        }
        //后将左节点压栈
        if(cur.left!=null){
            stack.push(cur.left);
        }
    }
}

后序遍历：

1. 用先序遍历的方式，但是先压cur的左节点，再压cur的右节点，每次弹出节点时，将其压入另一个栈B
2. 最后弹出栈B，得到的结果即后序遍历结果

实现代码

public static void stackLastPrint(Node cur){
    Stack<Node> stack1 = new Stack<Node>();
    Stack<Node> stack2 = new Stack<>();
    stack1.push(cur);//头结点先入栈
    while(!stack1.isEmpty()){
        cur = stack1.pop();
        stack2.push(cur);//将弹出的结点压入另一栈
        //先将左节点压栈
        if(cur.left!=null){
            stack1.push(cur.left);
        }
        //后将右节点入栈
        if(cur.right!=null){
            stack1.push(cur.right);
        }
    }
    //弹出栈2中的node
    while(!stack2.isEmpty()){
        System.out.print(stack2.pop().value+" ");
    }
}

中序遍历：

1. 先将根节点入栈
2. 将其所有左子节点入栈
3. 每次弹出一个节点，并打印
4. 然后对弹出节点的右子树重复1~3过程

实现代码

public static void stackMidPrint(Node cur){
        Stack<Node> stack = new Stack<>();
        //助理解写法
//        stack.push(cur);//先将头结点入栈
//        while(!stack.isEmpty()){
//            //将左子节点全部入栈（如果有）
//            while(cur.left!=null){
//                stack.push(cur.left);
//                cur = cur.left;
//            }
//            //出栈并打印
//            cur = stack.pop();
//            System.out.print(cur.value+" ");
//            //如果有右节点，将右节点入栈，并再次循环
//            if(cur.right!=null){
//                cur = cur.right;
//                stack.push(cur);
//            }
//        }
        //简洁写法
        while(!stack.isEmpty() || cur!=null){
            if(cur!=null){
                stack.push(cur);
                cur = cur.left;
            }else{
                cur = stack.pop();
                System.out.print(cur.value+" ");
                cur = cur.right;
            }
        }
    }

三、拓展

1、深度优先遍历

先序遍历

2、宽度优先遍历

使用队列

1. 先将头结点入队
2. 每次一个节点出队，并打印
3. 然后对出队节点左右节点入队，先入左，后入右
4. 重复2~3过程直到队空

结果：1 23 4567

实现代码

//宽度优先遍历
public static void breadthFirst(Node head){
    if(head == null) return;
    Queue<Node> queue = new LinkedList<Node>();
    queue.add(head);
    while(!queue.isEmpty()){
        Node cur = queue.poll();
        System.out.print(cur.value+" ");
        if(cur.left!=null){
            queue.add(cur.left);
        }
        if(cur.right!=null){
            queue.add(cur.right);
        }
    }
}

利用宽度优先遍历求二叉树的最大宽度：

• 利用HashMap结构：

实现代码

//计算二叉树最大宽度（使用Map集合）
public static Integer theMaxBreadth1(Node head){
    if(head == null) return 0;
    Queue<Node> queue = new LinkedList<Node>();
    HashMap<Node, Integer> map = new HashMap<>();
    Integer curLevel = 1; //当前层
    Integer curLevelNodes = 0; //当前层的节点数
    Integer max = Integer.MIN_VALUE;
    queue.add(head);
    map.put(head,curLevel);
    while(!queue.isEmpty()){
        Node cur = queue.poll();
        Integer curNodeLevel = map.get(cur);
        //如果是当前层节点，则当前层节点数+1
        if(curNodeLevel == curLevel){
            curLevelNodes++;
        }else{
            //如果不是当前层，说明已经来到下一层，curLevel+1，同时分析上一层节点数，并将当前层节点数重置为1
            curLevel++;
            max = Math.max(max,curLevelNodes);
            curLevelNodes = 1;
        }
        System.out.print(cur.value+" ");
        if(cur.left!=null){
            queue.add(cur.left);
            //如果有左节点则记录左节点的层数
            map.put(cur.left,curNodeLevel+1);
        }
        if(cur.right!=null){
            queue.add(cur.right);
            //如果有右节点则记录右节点的层数
            map.put(cur.right,curNodeLevel+1);
        }
    }
    max = Math.max(max,curLevelNodes);
    return max;
}

• 不使用其他结构

实现代码

public static Integer theMaxBreadth2(Node head){
    if(head == null) return 0;
    Queue<Node> queue = new LinkedList<>();
    queue.add(head);
    Node curLevelEndNode = head; //当前层的最后一个节点
    Node nextLevelEndNode = null; //下一层的最后一个节点
    Integer curLevelNodes = 0; //当前层节点数
    Integer max = Integer.MIN_VALUE;
    while(!queue.isEmpty()){
        Node cur = queue.poll();
        System.out.print(cur.value+" ");
        //如果有左右节点
        if(cur.left!=null){
            queue.add(cur.left);
            //更新下一层最后一个节点
            nextLevelEndNode = cur.left;
        }
        if(cur.right!=null){
            queue.add(cur.right);
            //更新下一层最后一个节点
            nextLevelEndNode = cur.right;
        }
        if(cur == curLevelEndNode){
            //如果当前节点是当前层最后一个节点，当前层节点数+1，然后更新max，最后将当前层节点数清空，并更新当前层最后节点，重置下一层最后节点
            curLevelNodes++;
            max = Math.max(max,curLevelNodes);
            curLevelNodes = 0;
            curLevelEndNode = nextLevelEndNode;
            nextLevelEndNode = null;
        }else{
            //如果当前节点不是当前层最后一个，当前层节点数+1
            curLevelNodes++;
        }
    }
    return max;
}

• 较简便的方法

实现代码

public static Integer theMaxBreadth3(Node head){
    if(head == null) return 0;
    Queue<Node> queue = new LinkedList<>();
    //头结点先入队
    queue.offer(head);
    int max = Integer.MIN_VALUE;
    while(!queue.isEmpty()){
        //记录本层的节点数，即队列中的节点数
        int levelNodes = queue.size();
        max = Math.max(levelNodes,max);
        //遍历本层每个节点，将其左右节点加入队列，每遍历一个就将这个节点出队
        for(int i = 0; i < levelNodes; i++){
            if(queue.peek().left!=null){
                queue.offer(queue.peek().left);
            }
            if(queue.peek().right!=null){
                queue.offer(queue.peek().right);
            }
            queue.poll();
        }
        //这样遍历完后，队列中就都是下一层的节点
    }
    return max;
}