与桶相关的排序

一、计数排序

基本思路

• 找出数组中最大和最小元素，并依次数据范围设定桶的数量
• 遍历数组，并统计每个元素出现的次数，保存到桶中
• 最后顺序输出每个桶（出现了多少次就输出几个该桶对应的元素）

缺点

• 依赖数据状况，数据范围比较大时，桶的数量就很多，很耗空间

动图演示

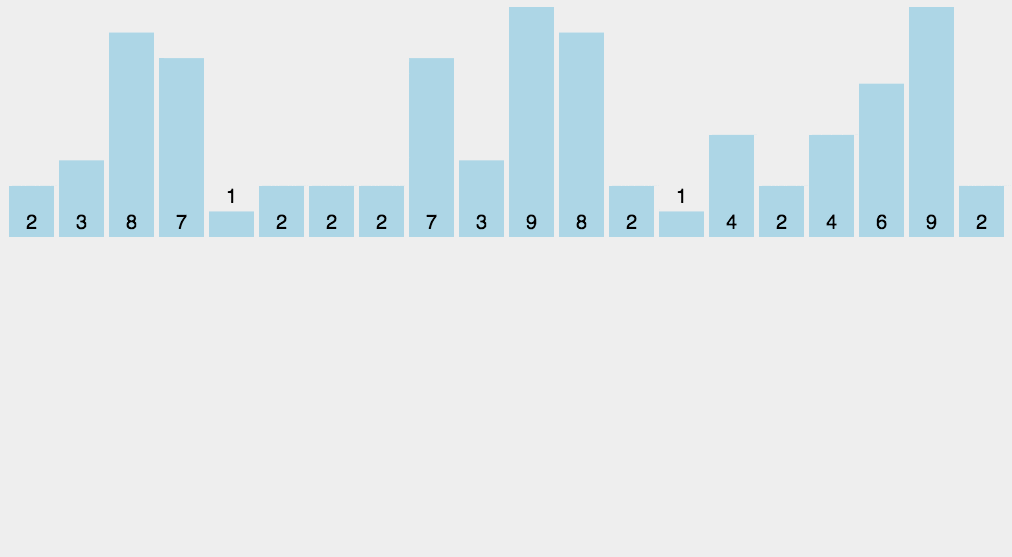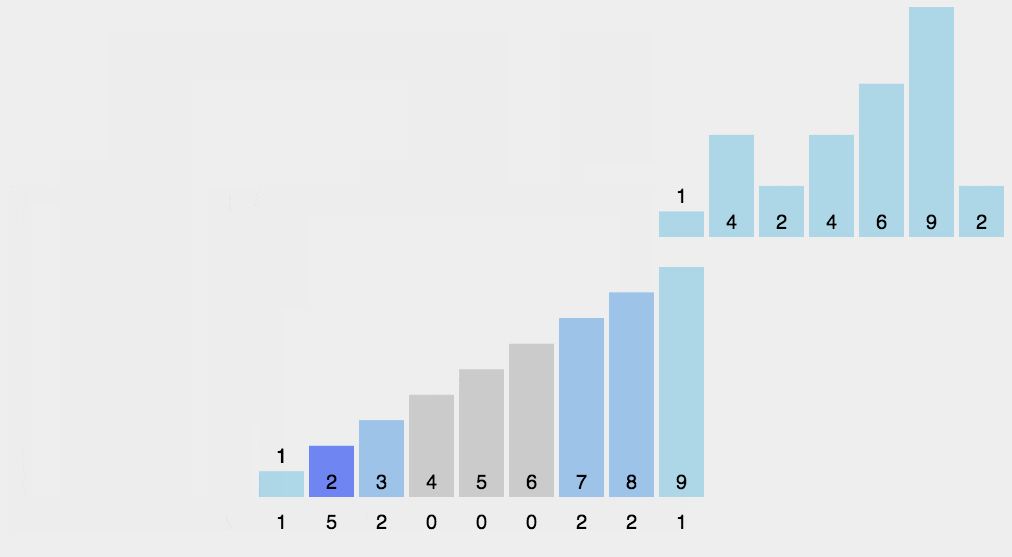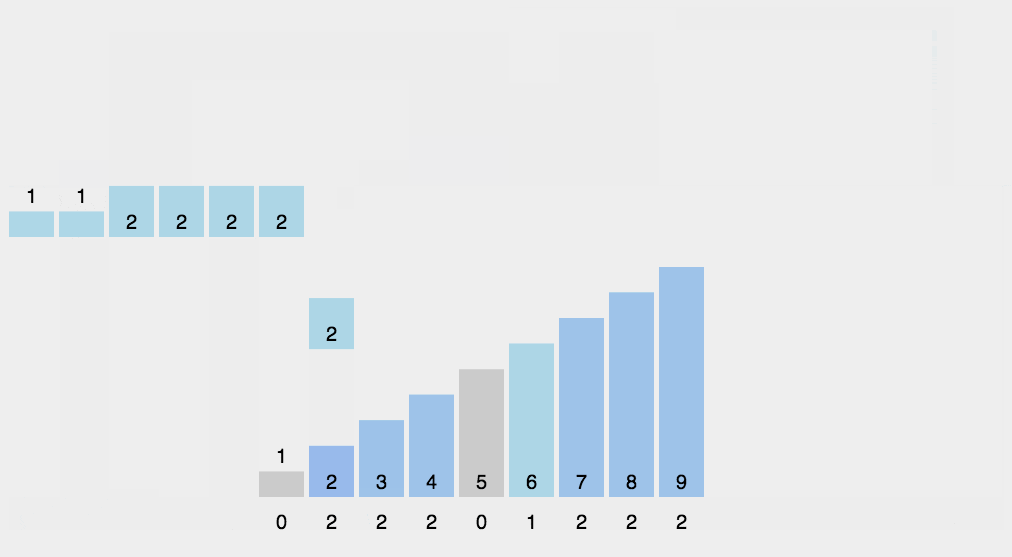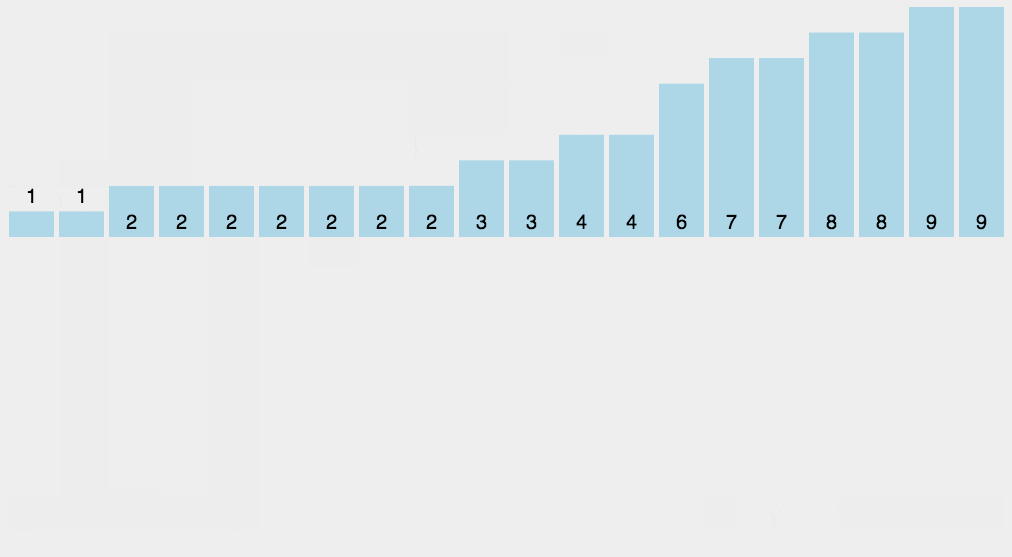
二、桶排序

基本思路

• 将数组中最大最小值找出，依次确定数据范围，并将此范围等分为几个区域
• 每个区域为一个桶，对每个桶的内部进行排序
• 最后根据桶的顺序输出每个桶内元素

示意图

将元素分布到桶中：

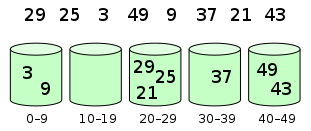
对每个桶进行排序：

三、基数排序

基本思路

• 以数字为例，遍历数组，并将元素放入与元素个位上的数对应的编号的桶中
• 遍历完后，按照先进先出的方式，按顺序将每个桶中的元素放入原数组
• 然后再遍历数组，并将元素放入与元素十位上的数对应的编号的桶中
• 依旧按先进先出方式，按顺序将每个桶中元素放入原数组
• 按以上方式，直到遍历完最高位

动图演示

实现代码（仅针对非负值进行排序）

//only for non-negative value，仅适用非负值
public static void radixSort(int[] arr){
    if(arr == null || arr.length < 2){
        return;
    }
    radix(arr,0,arr.length-1,maxbits(arr));
}
private static void radix(int[] arr, int L, int R, int digit){
    final int radix = 10;//基数
    int i=0,j=0;
    //辅助空间，数组有多少个数，辅助空间就多大
    int[] help = new int[R-L+1];
    //最大有多少位就遍历多少次,d为当前遍历的数据的位，1表示个位，以此类推
    for(int d = 1;d <= digit;d++){
        //计数空间大小为10
        //count[i]记录 d位数字 <= i 的个数
        //如d=1,i=2,count[2]记录原数组中个位数小于等于2的数的个数
        int[] count = new int[radix];
        //正序遍历数组，并记录count
        for(i = L;i <= R;i++){
            //得到数组中i位置数的第d位数
            j = getDigit(arr[i],d);
            count[j]++;
        }
        //将记录的数量往后叠加，变成 <= 的个数
        for(i = 1;i < radix;i++){
            count[i] = count[i]+count[i-1];
        }
        //逆序遍历数组，将元素放入桶（辅助空间）内对应的位置（该元素第d位数对应的count的数量-1），并将对应的count-1
        for(i = R;i >= L;i--){
            j = getDigit(arr[i],d);
            help[count[j]-1] = arr[i];
            count[j]--;
        }
        //将这次排好的数放回原数组
        for(i = L,j = 0;i <= R;i++,j++){
            arr[i] = help[j];
        }
    }
}
//取得数组中最大数的位数
private static int maxbits(int arr[]){
    int max = Integer.MIN_VALUE;
    for(int i = 0;i < arr.length;i++){
        max = Math.max(arr[i],max);
    }
    //记录位数
    int res = 0;
    while (max!=0){
        res++;
        max /=10;
    }
    return res;
}
//取得给定数的某一位的值,d=1表示个位，依次类推
private static int getDigit(int num, int d){
    return num / (int)(Math.pow(10,d-1)) % 10;
}